Skip to main content

Magnetic field :- parallel magnetic circuit

 Parallel Magnetic Circuit

Definition: A magnetic circuit having two or more than two paths for the magnetic flux is called a parallel magnetic circuit. Its behaviour can be compared to the parallel electric circuit. The parallel magnetic circuit contains different dimensional areas and materials having various numbers of paths.



The above figure shows a parallel magnetic circuit. In this circuit, a current-carrying coil is wound on the central limb AB. This coil sets up the magnetic flux φ1 in the central limb of the circuit. The flux φ1 which is in the upward direction is further divided into two paths namely ADCB and AFEB. The path ADCB carries flux φ2, and the path AFEB carries flux φ3. It is clearly seen fro the above circuit that

φ1 = φ2 + φ3

The two magnetic paths ADCB and AFEB form the parallel magnetic circuit, thus, the ampere-turns (ATs) required for this parallel circuit are equal to the ampere-turns (ATs) required for any one of the paths.

As we know, reluctance is

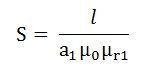
parallel-mag-ckt-eq-1
If S1 = reluctance of path BA will be

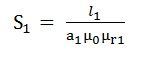
parallel-mag-ckt-eq2
S2 =reluctance of path ADCB will be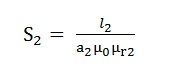
parallel-mag-ckt-eq3
S3 = reluctance of the path AFEB will be

parallel-mag-ckt-eq4

Therefore, the total MMF or the total Ampere turns required in the parallel magnetic circuit will be the sum of all the individual parallel paths.

Total mmf required = mmf required for the path BA +mmf required for the path ADCB + mmf required for the path AFEB

parallel-mag-ckt-eq5

Where φ1. Φ2, φ3 is the flux and S1, S2, S3 are the reluctances of the parallel path BA, ADCB and AFEB respectively

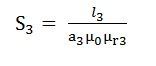
Comments

Post a Comment

Popular posts from this blog

Gtu sem 5th python programming ( 3151108 ) question paper download

Python programming (3151108)exam questions paper summer 2022. Gtu python programming paper download. plication (MCA) , PDDC , Diploma Of pharmacy (D.pharm) , Diploma engineering. While you searched for download GTU B.E. CIVIL SEM 5 3151108 Python Programming gtupaper.in past exam papers.You might have gone to other sites on the internet along with the official gtu site i.e. gtu.ac.in but you must be confused there with your download GTU B.E. CIVIL SEM 5 3151108 Python Programming gtupaper.in past exam papers. AS you dont know the subject code of GTU B.E. CIVIL SEM 5 3151108 Python Programming gtupaper.in .That`s what we were filling lack of. So we created sudybudyy.in   Hey students, simply long press on image to download , you get download image option.   Here, on gtupaper.in You don`t need to remember your GTU B.E. CIVIL SEM 5 3151108 Python Programming gtupaper.in subject code.You just select your branch from be , bpharm , mba , mca , dpharm , mpharm , pddc , me and diploma...
Post a Comment
Read more

what is Integration in maths

  Integration in Mathematics Integration is a fundamental concept in calculus that represents the accumulation of quantities. It is the reverse process of differentiation and is used to find areas, volumes, central points, and many other useful things. 1. Why is Integration Important? Finds Area under curves. Calculates Volume in 3D spaces. Solves Differential Equations in physics and engineering. Used in Probability & Statistics for continuous distributions. 2. Types of Integration 1️⃣ Indefinite Integral (Without Limits) Represents the antiderivative of a function. Formula: ∫ f ( x ) d x = F ( x ) + C \int f(x) dx = F(x) + C where C C is the constant of integration. Example: ∫ x 2 d x = x 3 3 + C \int x^2 dx = \frac{x^3}{3} + C 2️⃣ Definite Integral (With Limits) Computes a numerical value over an interval [ a , b ] [a, b] . Formula: ∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_{a}^{b} f(x) dx = F(b) - F(a) Example: ∫ 0 3 x 2 d x = [ x 3 3 ...
Post a Comment
Read more

What is unit vector :- explain unit vector

Electromagnetic fields Unit vector- A unit vector has a function to indicate the direction. Its magnitude is always unity, irrespective of the direction which it indicates and the co-ordinate system under consideration. Thus for any vector, to indicate its direction a unit vector can be used. Consider a unit vector āoA in the direction of OA as shown in o the Fig. This vector indicates the direction of OA but its magnitude is unity. Fig Unit vector aOA So vector OA can be represented completely as its magnitude R and the direction indicated by unit vector along its direction. ŌĀ = |OA| āOA =R āOA āOA=1
Post a Comment
Read more